Lecture 19 — Search

Overview

• Notion of an algorithm
• Problems:
  • Finding the two smallest values in a list
  • Finding the index of a particular value in a list
  • Finding the index of a particular value in a sorted list
  • Sorting a list (Lecture 20)
• Analyzing our solutions:
  • Mathematically
  • Experimental timing

Material for Lectures 19 and 20 is in Chapters 10 and 11 of the text.

Algorithm

• Precise description of the steps necessary to solve a computing problem
• Description is intended for people to read and understand
• Gradual refinement:
  • Starts with English sentences
  • Gradually, the sentences are made more detailed and more like programming statements
  • Allows us to lay out the basic steps of the program before getting to the details.
• A program is an implementations of one or more algorithms.

Multiple Algorithms

• Often there are many different algorithms that can solve a problem.
• They differ in:
  • Ease of understanding
  • Ease of implementation
  • Efficiency
• All three considerations are important and their relative weight depends on the context.

Problem 1: Finding the Two Smallest Values in a List

• Given a list of integers, floats, or any other values that can be compared with a less than operation, find the two smallest values in the list
• We need to be careful with this problem formulation: are duplicates allowed? does it matter?

Exercise

1. Outline two or more approaches to finding the indices of the two smallest values in a list.
2. Think through the advantages and disadvantages of each approach.
3. Write a more detailed description of the solutions.
4. How might your approaches change if we just have to find the values and not the indices?

Evaluating Our Solutions Analytically

We’ve already covered this briefly in Lecture 13.

• Count the number of steps as a function of the size of the list.
  • Usually we use 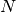as a variable to indicate this size.
• Informally, if the number of operations is (roughly) proportional to 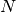we write 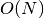(read as “order of N”)
• If the number of operations is proportional to 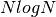we write .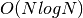
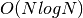  • Importantly, the best sorting algorithms are .
• We will informally apply this analysis to our solution approaches.

Evaluating Our Solutions Experimentally

• Needs:
  • generate example data, and
  • time our algorithm implementations.
• Experimental data can be generated using the random module. We will make use of
  • randrange
  • shuffle
• Timing uses the time module and its time function, which returns the number of seconds (as a float) since an arbitrary start time called an “epoch”.
  • We will compute the difference between a start time and an end time as our timing measurement.

Exercise

• Implement two (or more) algorithms to find the indices of the two smallest values in the list:

  import random
  import time
  
  def index_two_v1( values ):
      pass   # don't do anything; using 'pass' prevents syntax errors
  
  
  
  
  
  def index_two_v2( values ):
      pass
  
  
  
  
  
  
  
  if __name__ == "__main__":
      n = int(raw_input("Enter the number of values to test ==> "))
      values = range(0,n)
      random.shuffle( values )
  
      s1 = time.time()
      (i0,i1) = index_two_v1(values)
      t1 = time.time() - s1
      print "Ver 1:  indices (%d,%d); time %.3f seconds" %(i0,i1,t1)
  
      s2 = time.time()
      (j0,j1) = index_two_v2(values)
      t2 = time.time() - s2
      print "Ver 2:  indices (%d,%d); time %.3f seconds" %(j0,j1,t2)
  

We will experiment with at least two implementations.

Searching for a Value

• Problem: given a list of values, L, and given a single value, x, find the (first) index of x in L or determine that x is not in L.
• Basic algorithm is straightforward, and require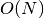s steps
• We can solve this in Python using a combination of in and find, or by writing our own loop.
  • The text book discusses a number of variations on the algorithm.

Exercises

1. Write a Python function called linear_search that returns the index of the first instance of x in L or determines that it is not there (and returns a -1).

2. What if the list is already sorted? Write a modifed version of linear_search that returns the index of the first instance of x or the index where x should be inserted if it is not in L For example, in the list

   L = [ 1.3, 7.9, 11.2, 15.3, 18.5, 18.9, 19.7 ]
   

   the call

   linear_search(11.9, L)
   

   should return 3.

Binary Search

• If the list is ordered, do we have to search it by looking at location 0, then 1, then 2, then 3, ...?
• What if we looked at the middle location first?
  • If the value of x is greater than that value, we know that the first location for x is in the upper half of the list.
  • Otherwise, the first location for x is in the lower half of the list
• In other words, by making one comparison, we have eliminated half the list in our search!
• We can repeat this process of “halving” the list until we reach just one location.

Algorithm and Implementation

• We need to keep track of two indices:

  • low: all values in the list at locations 0..low-1 are less than x
  • high: all values in the list at locations high ..N are greater than or equal to x. Write N as the length of the list.

• Initialize low = 0 and high = N.

• In each iteration of a while loop

  • Set mid to be the average of low and high.
  • Update the value of low or high based on comparing x to L[mid].

• Here is the actual code:

  def binary_search( x, L):
      low = 0
      high = len(L)
      while low != high:
          mid = (low+high)/2
          if x > L[mid]:
              low = mid+1
          else:
              high = mid
      return low
  

Exercises

1. Using

   L = [ 1.3, 7.9, 11.2, 15.3, 18.5, 18.9, 19.7 ]
   

   what are the values of low, high and mid each time through the while loop for the calls

   binary_search( 11.2, L )
   
   
   
   binary_search( 19.1, L )
   
   
   
   binary_search( -1, L)
   
   
   
   
   binary_search( 25, L)
   

2. How many times will the loop execute f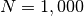or or 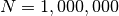? (You will not be able to come up with an exact number, but you should be able to come close.) How does this compare to the linear search?

3. Would the code still work if we changed the > to the >=? Why?

4. Modify the code to return a tuple that includes both the index where x is or should be inserted and a boolean that indicates whether or not x is in the list.

We will also perform experimental timing runs if we have time at the end of class.

Summary

• Algorithm vs. implementation
• Criteria for choosing an algorithm: speed, clarity, ease of implementation
• Timing/speed evaluations can be either analytical or experimental.
• Searching for indices of two smallest values
• Linear search
• Binary search of a list that is ordered.