Linked Lists I

Advanced Programming---CSCI-6090

See also SGI's STL Programmer's Guide description of lists; or Austern, Generic Programming and the STL, Chapter 5 and Sections 9.1, 9.2, and 16.1.2.

Linked lists are one of the most useful ways of representing linear sequences of data. Linked lists are the sequence representation of choice when many insertions and/or deletions are required in interior positions and there is little need to jump around randomly from one position to another. That's because

We now want to look beyond these basic facts and examine in detail how linked-list manipulation can be implemented. The issues we should try to understand about linked list implementations include:

We will look at the Hewlett-Packard (HP) STL list class source code, or actually a slightly reorganized and simplified version of it. (HP STL was the basis for most STL implementations. Later implementations of STL lists differ most significantly from HP's in the way they handle storage management.)

First, here is an overview of how the HP STL list class implementation stacks up in terms of the issues mentioned above:

For this discussion we will refer to a modified version of the Hewlett-Packard STL source code for the list class, contained in the following files: This code is based on the Hewlett-Packard STL distribution and is functionally identical to it except that all dependence on allocators has been removed in order to make the code more self-contained. This change does not affect the efficiency of the implementation; it only makes it a little less flexible (the use of allocators in STL containers makes them easily adaptable to different memory models such as those supported by Borland's older 16-bit compilers). There are also some changes in organization of the code to make it easier to read and understand, the main one being that the special list memory management code has been moved out of the list class into the separate list_memory_manager class in memman.h.

STL List Node Representation

The list class definition begins with the definition of the node structure used for the doubly-linked representation: template <class T> class list { protected: // Representation (doubly linked): struct list_node { list_node* next; list_node* prev; T data; }; ... This struct is defined in a protected part of the class; it is not public because it is better not to give the list user direct access to the representation (information hiding), and protected is better than private in that any class derived from list will have access to the representation.

Type definitions

The next part of the list class definition is a series of typedefs of identifiers that are required to be defined by the STL specifications for sequence containers (value_type, reference, const_reference, size_type, and difference_type) or for internal use (pointer, link_type, and list_memory_manager_type). ... public: // Types: typedef T value_type; typedef T& reference; typedef const T& const_reference; typedef size_t size_type; typedef ptrdiff_t difference_type; private: typedef T* pointer; typedef list_node* link_type; typedef list_memory_manager<list_node> list_memory_manager_type; ... The last three types are intended for internal use only and thus are put in the private part of the class definition.

Data members

Next we have the data members of list objects: ... protected: link_type node; size_type length; static size_type number_of_lists; static list_memory_manager_type manager; ... We will see that node is a pointer to the header node of the list and length is maintained as the number of data elements in the list. The static member number_of_list keeps track of how many lists are in existence, so that when the number becomes zero the storage manager can clean everything up. Finally, storage management routines are accessed through the static member manager. (Recall that a static member is shared by all objects of the class, rather than one per object.)

Iterators

The next section consists of a nested class definition or a typedef for each of the four kinds of list iterators. ... public: // Iterator types (defined by nested classes and typedefs) // class iterator; // class const_iterator; // class reverse_iterator; // class const_reverse_iterator; #include "listiter.h" ... We will come back to these definitions later.

Member functions

The rest of the class definition contains the interfaces of all of the member functions, including constructors, destructor, assignment and swap operations, queries (or accessors), insertion, erasure, and special list functions (splicing, removal, merging, and sorting). In a few cases the bodies are given inline, but for most of the operations the bodies are given in the separate file list.C.

Constructors

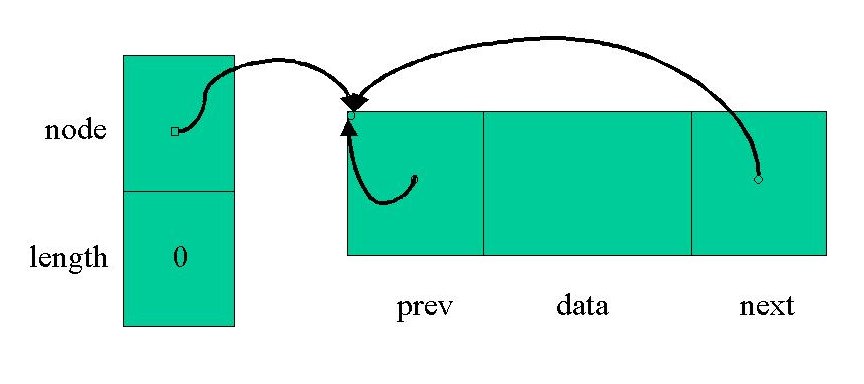
Turning to the file list.C, let's see how the default constructor is implemented: ... // Default constructor: template <class T> inline list<T>::list() : length(0) { ++number_of_lists; node = manager.get_node(); node->next = node; node->prev = node; } ... This constructor initializes the list with 0 for its length member, increments number_of_lists (which is initialized to zero with a static member initialization at the end of list.C), initializes node with a pointer to a new list_node returned by manager.get_node, and sets the next and prev members of the node to point to the node itself. For the moment, think of manager.get_node() as being a call to new list_node; we will go into how it really works later.

The other constructors are defined in terms of one of the insert member functions, so let us turn now to those functions.

Insertion

For understanding the code in the insert member functions we need to know just a little about the representation of iterators, namely that each iterator object maintains its current place in a list with a data member called current holding a link_type pointer to a node of the list. template <class T> inline list<T>::iterator list<T>::insert(iterator position, const T& x) { link_type tmp = manager.get_node(); new (&(tmp->data)) T(x); tmp->next = position.current; tmp->prev = (position.current)->prev; (position.current)->prev->next = tmp; (position.current)->prev = tmp; ++length; return tmp; } The line new (&(tmp->data)) T(x); is a little unusual and will be more easily understood after we've gone over memory management. For now let's just assume it is equivalent to tmp->data = x; The rest of the code contains a lot of pointer manipulation, but it's easy to see what it does if we draw the nodes and pointers and see how they change as each assignment is executed. The nice part about it is that there are no special cases to check for; that's one of the advantages of having a header node.

Exercise: Do this hand simulation of the insert operation on an empty list (as initialized above with list()), T equal to int, position equal to begin() and x equal to 3. The other STL list function implementations are in file list.C.

Insert members

So far we've looked at the implementation of the basic list insert member function. The list class also defines several other insert members and implements them in terms of the basic one: template <class T> void list<T>::insert(iterator position, const T* first, const T* last) { while (first != last) insert(position, *first++); } template <class T> void list<T>::insert(iterator position, const_iterator first, const_iterator last) { while (first != last) insert(position, *first++); } template <class T> void list<T>::insert(iterator position, size_type n, const T& x) { while (n--) insert(position, x); }

Other constructors

The other list constructors besides the default constructor are defined in terms of the above insert members: // Construct a list of n elements, each a copy of a given value: template <class T> //inline list<T>::list(size_type n, const T& value = T()) : length(0) { inline list<T>::list(size_type n, const T& value) : length(0) { ++number_of_lists; node = manager.get_node(); node->next = node; node->prev = node; insert(begin(), n, value); } // Construct a list initialized to a given range of values: template <class T> inline list<T>::list(const T* first, const T* last) : length(0) { ++number_of_lists; node = manager.get_node(); node->next = node; node->prev = node; insert(begin(), first, last); } // Copy constructor: template <class T> inline list<T>::list(const list<T>& x) : length(0) { ++number_of_lists; node = manager.get_node(); node->next = node; node->prev = node; insert(begin(), x.begin(), x.end()); } Before looking at the destructor, let's examine the erase operations, since the destructor uses one of them.

Erasure

Erasure of an item pointed to by an iterator is done by relinking the surrounding nodes to point to each other instead of the node containing the item, then cleaning up that node and returning it to the storage manager: template <class T> inline void list<T>::erase(iterator position) { (position.current)->prev->next = (position.current)->next; (position.current)->next->prev = (position.current)->prev; (position.current)->data.~T(); manager.put_node(position.current); --length; } Note that if T is instantiated with a built in type such as int, the destructor call is to ~int(), a function that doesn't exist. This looks like a problem, but in fact the compiler is supposed to ignore it and generate no code for the call. (xlC issues a warning, but it shouldn't.)

Instead of the destructor call and the call of manager.put_node the more usual storage management procedure would be to call

delete position.current; This would first call (position.current)->~link_node(), and then return the node to the standard storage deallocator. In struct link_node (defined in list.h), we didn't define ~link_node(), but the default destructor definition supplied by the compiler calls the destructor of each member that can have one. In this case, the data member is the only one that can have a destructor (pointers cannot), so the definition supplied by the compiler is equivalent to ~link_node() { data.~T(); } So our explicit destructor call (position.current)->data.~T(); takes care of this chore, and manager.put_node(position.current); disposes of the node itself, in a much more efficient way than the standard storage deallocator would (as we will see when we look at the list_memory_manager class).

Exercise: Interesting cases to consider are when one or both of the surrounding nodes are the header (that is, the node being erased is the first, last, or only data node in the list). Verify by hand simulation that the code works perfectly well in these cases even though it has no special checks for them. (This is another advantage of the header node and also of circular linking.)

There is one other erase member function:

template <class T> void list<T>::erase(iterator first, iterator last) { while (first != last) erase(first++); }

Destructor

The list destructor uses the second erase member to erase all elements of the list (thus calling ~T() on each data element). It then returns the header node to the storage allocator and decrements number_of_lists. If this was the last list, the next line "turns out the lights" (deallocates all of the space allocated for list nodes). template <class T> inline list<T>::~list() { erase(begin(), end()); manager.put_node(node); if (--number_of_lists == 0) manager.deallocate_buffers(); } Exercise: Consider the case in which T is list<int> , as in list< list<int> > list1; Suppose several list<int> values have been created and inserted in list1. What happens, in terms of erase and destructor calls, when list1 goes out of scope?

Assignment and swap operations

The code for the assignment operation is interesting because of the way it reuses list nodes that make up the left hand operand of the assignment. template <class T> list<T>& list<T>::operator=(const list<T>& x) { if (this != &x) { iterator first1 = begin(); iterator last1 = end(); const_iterator first2 = x.begin(); const_iterator last2 = x.end(); while (first1 != last1 && first2 != last2) *first1++ = *first2++; if (first2 == last2) erase(first1, last1); else insert(last1, first2, last2); } return *this; } Note that the code first checks if the left and right operands of operator= are the same object; if so, it does nothing. This check is necessary because executing the rest of the code would be incorrect if both operands were the same object.

The first part of the code, through the while loop, copies as much of the right hand list (x) as will fit into the nodes of the left hand list (this). If the end of x is reached before the end of the left hand list, the remainder of the left hand list is erased; otherwise, the remainder of x is copied onto the end of the left hand list.

This technique minimizes the number of calls to the storage manager.

Swap operation

Swapping two lists could be done with the STL generic swap function: template <class T> inline void swap(T& a, T& b) { T tmp = a; a = b; b = tmp; } Note, though, that when T is list<U> this uses three list<U> assignments, each of which involves copying all of the U values in one list to another. It is much more efficient just to swap the data members of the two lists: template <class T> inline void list<T>::swap(list<T>& x) { ::swap(node, x.node); ::swap(length, x.length); } The notation ::swap indicates that the globally defined swap function should be used in these calls.

Auxiliary function, transfer, for implementing special list operations

The transfer operation alters a list by inserting into it a segment removed from another list. It is not one of the list public members, but it is used in implementing the public splice, merge, and reverse operations. It is similar to insert but involves no copying of data or allocation of nodes; instead it re-links a segment of nodes out of one list and into another, modifying both lists (which might in fact be the same list). template <class T> inline void list<T>::transfer(iterator position, iterator first, iterator last) { (last.current)->prev->next = position.current; (first.current)->prev->next = last.current; (position.current)->prev->next = first.current; link_type tmp = (position.current)->prev; (position.current)->prev = (last.current)->prev; (last.current)->prev = (first.current)->prev; (first.current)->prev = tmp; } As with insert, there is a lot of pointer manipulation, but it is not difficult to see how it works:

Exercise: Do a hand simulation of the transfer operation on list1 containing 1 2 3 4 and list2 containing 11 12 13 14 15 16, with position pointing to (the node containing) 2, first pointing to 12, and last pointing to 15. After the transfer operation, list1 should contain 1 12 13 14 2 3 4 and list2 should contain 11 15 16. Note that the item pointed to by last (15) is not part of the segment transfered.

The main thing to note about transfer is that since it only does a constant number of pointer assignments, it is a constant time operation. If first and last define a long segment it is much more efficient to move that segment via transfer than it would be to copy it, since copying would have to take linear time. On the other hand, using transfer is inappropriate if the original value of the source list is needed in later calculations. In that case copying (with insert(position, first, last)) should be done instead.

Splicing

The splice operations, which are described and illustrated in SGI's STL Programmer's Guide description of lists, are easily implemented in terms of transfer. template <class T> inline void list<T>::splice(iterator position, list<T>& x) { if (!x.empty()) { transfer(position, x.begin(), x.end()); length += x.length; x.length = 0; } } template <class T> inline void list<T>::splice(iterator position, list<T>& x, iterator i) { iterator j = i; if (position == i || position == ++j) return; transfer(position, i, j); ++length; --x.length; } template <class T> inline void list<T>::splice(iterator position, list<T>& x, iterator first, iterator last) { if (first != last) { if (&x != this) { difference_type n = 0; distance(first, last, n); x.length -= n; length += n; } transfer(position, first, last); } } In the last version of splice we have to count the number of nodes from first to last in order to update the lengths of the two lists. Note that this is necessary only if two different lists are involved (determined with the test (&x != this)). In this case, splice takes linear, rather than constant, time.

Sorting

Of the remaining operations the most algorithmically interesting is sort. It is a form of merge sort, with the merging done bottom-up, nonrecursively. The key idea of the algorithm is ensuring that merges are done on two equal-length lists whenever possible, by maintaining a number of lists separately according to their length until they can be combined with other lists of the same length. The lists are maintained in an array called counter, with counter[i] either empty or holding a list of length 2i. This array is so named because its changing state resembles the state of a binary counter as it is being incremented. Merging of two equal-length lists produces a "carry" into the next position. The carry either occupies that position if it is currently empty, or it is merged with the nonempty list in that position, producing another carry, and so on. template <class T> void list<T>::sort() { if (size() < 2) return; list<T> carry; list<T> counter[64]; int fill = 0; while (!empty()) { carry.splice(carry.begin(), *this, begin()); int i = 0; while(i < fill && !counter[i].empty()) { counter[i].merge(carry); carry.swap(counter[i++]); } carry.swap(counter[i]); if (i == fill) ++fill; } for (int i = 1; i < fill; ++i) counter[i].merge(counter[i-1]); swap(counter[fill-1]); } Exercise: Hand simulate this algorithm with a list containing 14 8 9 5 11 2 4 15 1 3 6 12 7. Show the counter array contents after each iteration of the main while loop.

Exercise: The counter array used in this algorithm has a fixed size of 64. Is there any danger of running off the end of the array? Explain.

Exercise: Show that the computing time for this algorithm is O(n log n).