Skip to main content

Homework 6: Delaunay Triangulation

Part 1: Book Problems

Prepare a PDF file named hw6_delaunay_triangulation.pdf with your answers to the book problems below. You may use Latex, Google Docs (export/save as PDF), MS Word (export/save as PDF), and/or legibly handwrite on paper and scan to PDF.

From "Computational Geometry: Algorithms and Applications", de Berg, Cheong, van Kreveld, and Overmars.

You may discuss these problems with your classmates, but you must write up your solutions individually. Note the names of anyone you talked to or collaborated with in your hw6_delaunay_triangulation.pdf writeup.

Please do not search for solutions or notes published by the authors or any instructor or notes or solutions shared by other students on the internet. Any use of these types of materials is considered a violation of Academic Integrity for this course.

9.1
In this exercise we look at the number of different triangulations that a set of n points in the plane may allow.
a. Prove that no set of n points can be triangulated in more than ways.
b. Prove that there are sets of n points that can be triangulated in at least different ways.

9.13
The Gabriel graph of a set P of points in the plane is defined as follows: Two points p and q are connected by an edge of the Gabriel graph if and only if the disc with diameter pq does not contain any other point of P.
a. Prove that the Delaunay Graph, DG(P), contains the Gabriel graph of P.
b. Prove that p and q are adjacent in the Gabriel graph of P if and only if the Delaunay edge between p and q intersects its dual Voronoi edge.
c. Give an O(n log n) time algorithm to compute the Gabriel graph of a set of n points.

9.17
The weight of a triangulation is the sum of the lengths of all edges of the triangulation. A minimum weight triangulation is a triangulation whose weight is minimal. Disprove the conjecture that the Delaunay triangulation is a minimum weight triangulation.

Part 2: CGAL Programming Task

The coding activity for this assignment is based on Book Problem 9.3:
Prove that any two triangulations of a planar point set can be transformed into each other by edge flips. Hint: Show first that any two triangulations of a convex polygon can be transformed into each other by edge flips.

Your task is to write a program that takes 3 arguments on the command line. The first two command line arguments are input files that store initial and target triangulation. Each triangulation file lists first the 2D coordinates of the vertices, then the triangles that connect the vertices. You may assume that the vertex lists in the two input files are identical. The third command line argument is the name of the output file. You will output the sequence of edge flips that are necessary to transform the first triangulation to the second triangulation.

Here is a very small example mesh: 

  ./retriangulation input_small1.off input_small2.off output_small_1_to_2.txt

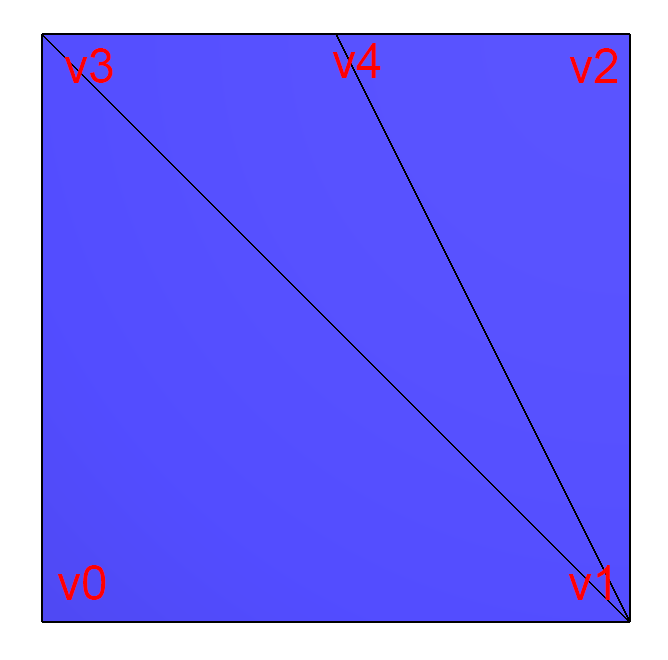
You are encouraged to use visualizations similar to the above images to help with debugging, but they are not part of the required assignment. The output file will contain the sequence of necessary "edge flips": 

  v1-v3 -> v0-v4
  v1-v4 -> v0-v2

And here is a slightly larger example: 

  ./retriangulation input_sample2.off input_sample3.off output_sample_2_to_3.txt

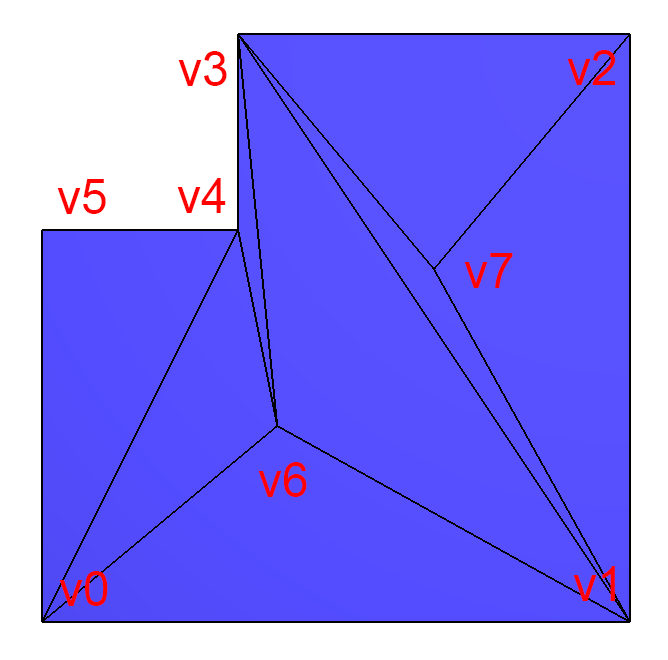
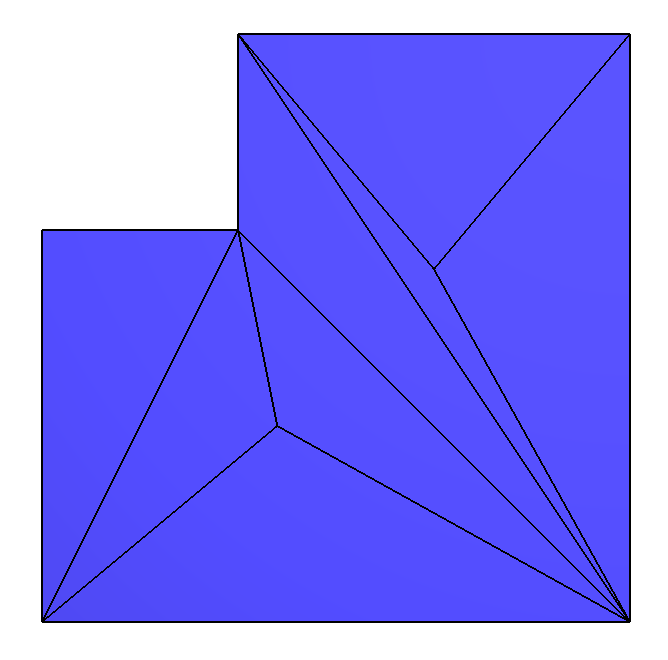
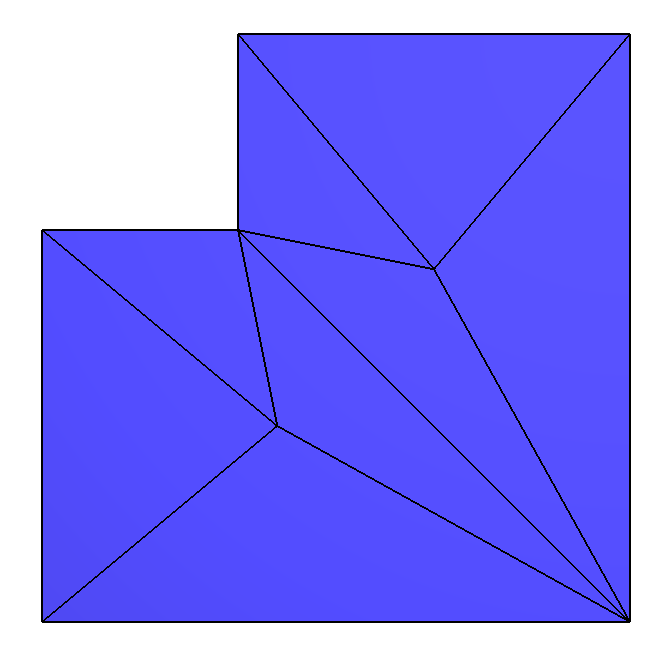
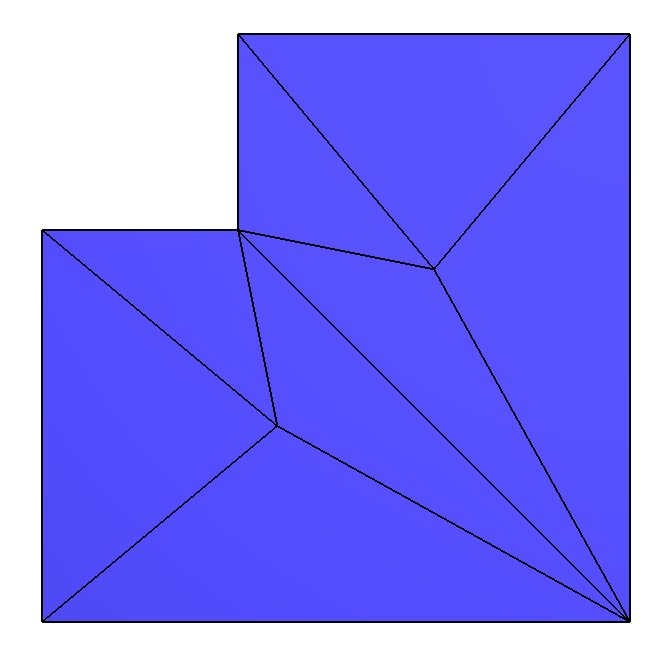
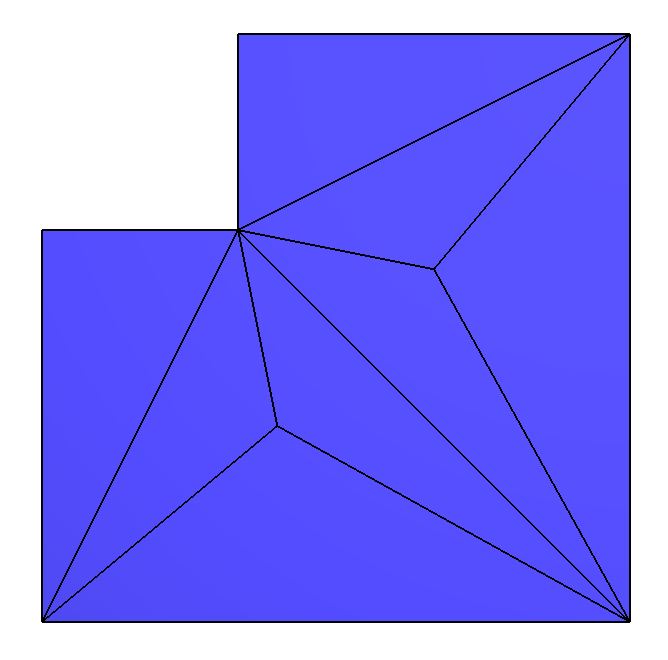
With this text output file: 

  v3-v6 -> v1-v4
  v0-v4 -> v5-v6
  v1-v3 -> v4-v7
  v1-v4 -> v6-v7
  v6-v7 -> v1-v4
  v5-v6 -> v0-v4
  v3-v7 -> v2-v4

Note that while the previous example does transform one mesh to the other, it is not in fact the minimum number of flips -- there are some unnecessary changes that are reverted later in the sequence. For extra credit you can optimize your program to produce fewer or minimal edge flips.