Homework 4: Half-Spaces & k-D Trees

Part 1: Book Problems

Prepare a PDF file named hw4_halfspaces_kdtrees.pdf with your answers to the book problems below. You may use Latex, Google Docs (export/save as PDF), MS Word (export/save as PDF), and/or legibly handwrite on paper and scan to PDF.

From "Computational Geometry: Algorithms and Applications", de Berg, Cheong, van Kreveld, and Overmars.

You may discuss these problems with your classmates, but you must write up your solutions individually. Note the names of anyone you talked to or collaborated with in your hw4_halfspaces_kdtrees.pdf writeup.

Please do not search for solutions or notes published by the authors or any instructor or notes or solutions shared by other students on the internet. Any use of these types of materials is considered a violation of Academic Integrity for this course.

4.1
In this chapter we studied the casting problem for molds of one piece. A sphere cannot be manufactured in this manner, but it can be manufactured if we use a two-piece mold. Give an example of an object that cannot be manufactured with a two-piece mold, but that can be manufactured with a three-piece mold.

4.10
Let H be a set of at least three half-planes with a non-empty intersection such that not all bounding lines are parallel. We call a half-plane h ∈ H redundant if it does not contribute an edge to ∩ H. Prove that for any redundant half-plane h ∈ H there are two half-planes h', h'' ∈ H such that h' ∩ h'' ⊂ h. Give an O(n log n) time algorithm to compute all redundant half-planes.

4.13
In the text we gave a linear time algorithm for computing a random permutation. The algorithm needed a random number generator that can produce a random integer between 1 and n in constant time. Now assume we have a restricted random number generator available that can only generate a random bit (0 or 1) in constant time. How can we generate a random permutation with this restricted random number generator? What is the running time of your procedure?

Part 2: CGAL Programming Task

Lidar or "light detection and ranging" technology is used to collect 3D points, a.k.a., a point cloud, of objects in the world around us. It can be used to scan the exteriors or interiors of buildings, as shown in the examples below. Note that the scan points have some uncertainty or noise in the point position and we have holes or missing data when objects are occluded or shadowed by other parts of the scene.

A common task is to collect all points near a query point x,y,z and estimate the local surface geometry, specifically the surface normal. This is helpful in eventually accomplishing the ultimate goal of converting the point cloud to a polygonal surface mesh.

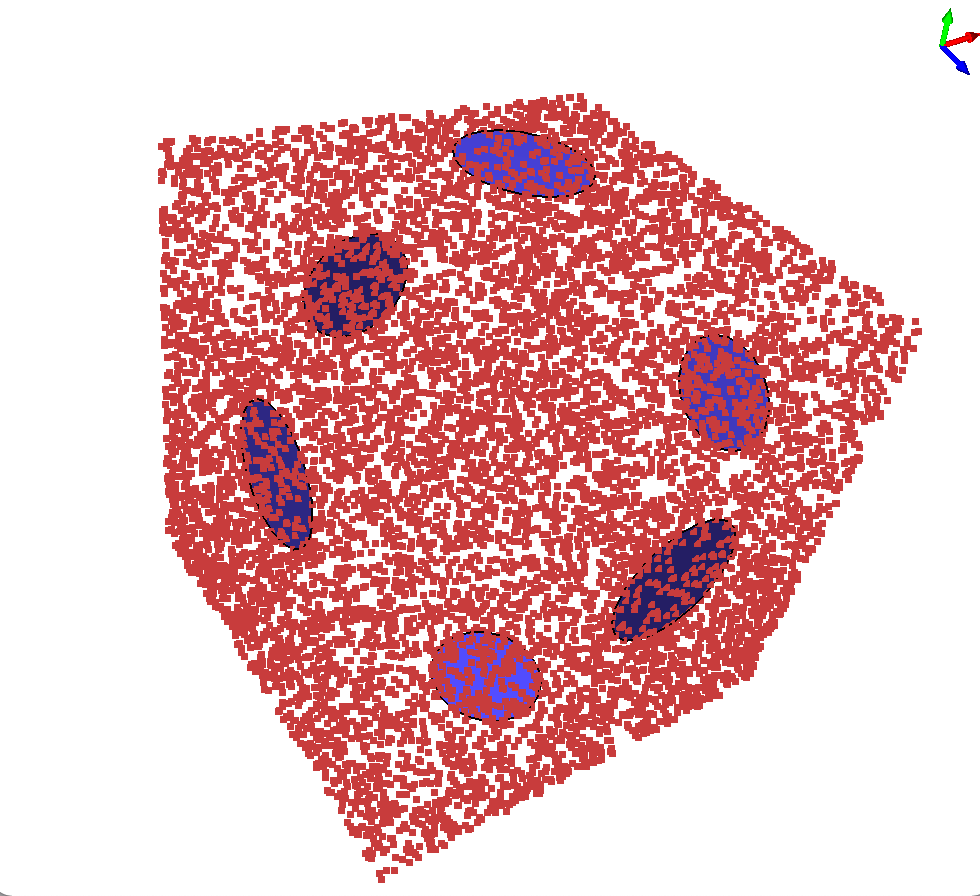
Your task is to write a program that loads a point cloud, a large set of 3D points, from an input file and store them in a CGAL kD tree. You will then process a list of queries against the kD tree one at a time. For each of these query points you will collect the c data points closest to that query position and give a rough estimate of the surface geometry at that position. We will assume that the surface is axis-aligned -- that is, it is parallel to the xy, yz, or xz plane.

For each query point you will output the best match plane (xy, yz, or xz), and the minimum radius necessary to capture exactly c points within a circle of that radius in the specified plane, with a tolerance or error in the perpendicular axis of no more than plus or minus t units. The values of c and t will be provided on the command line.

For example, we will start with a point cloud of 10,000 randomly distributed points on the surface of a cube from (-10,-10,-10)->(10,10,10). We are given 6 query points, one near the middle of each of the 6 faces of the cube. Once we determine the best matching axis-aligned plane, we determine the tightest radius around that query point that captures c=100 points with tolerance +/- 0.01 distance from that plane.

  ./detect_point_cloud_surface input_cube_points.txt input_cube_queries.txt 100 0.01 output_cube_stats.txt

After outputting the statistics file above, your program can use the CGAL Surface Mesh visualization to draw a simple polygonal representation of the circles, as shown below. Note that pressing 'v' will draw the vertices.

Additional input and output files coming soon

Part 3: Analysis of Implementation

In your hw4_halfspaces_kdtrees.pdf file, analyze the running time of your implementation for Part 2, in terms of n, the number of points in the point cloud, and c the number of points that must be collected. You may introduce other variables as necessary.