Skip to main content

Homework 3: Polygon Triangulations

Part 1: Book Problems

Prepare a PDF file named hw3_polygon_triangulations.pdf with your answers to the book problems below. You may use Latex, Google Docs (export/save as PDF), MS Word (export/save as PDF), and/or legibly handwrite on paper and scan to PDF.

From "Computational Geometry: Algorithms and Applications", de Berg, Cheong, van Kreveld, and Overmars.

You may discuss these problems with your classmates, but you must write up your solutions individually. Note the names of anyone you talked to or collaborated with in your hw3_polygon_triangulations.pdf writeup.

Please do not search for solutions or notes published by the authors or any instructor or notes or solutions shared by other students on the internet. Any use of these types of materials is considered a violation of Academic Integrity for this course.

3.2
A rectilinear polygon is a simple polygon of which all edges are horizontal or vertical. Let P be a rectilinear polygon with n vertices. Give an example to show that n/4 cameras are sometimes necessary to guard it.
Prepare a diagram of this example and include it in your .pdf. Your diagram may be digitally drawn or hand-drawn and photographed or scanned.

3.5
Give the pseudo-code of the algorithm to compute a 3-coloring of a triangulated simple polygon. The algorithm should run in linear time.

3.14
Given a simple polygon P with n vertices and a point p inside it, show how to compute the region inside P that is visible from p.

Part 2: CGAL Programming Task

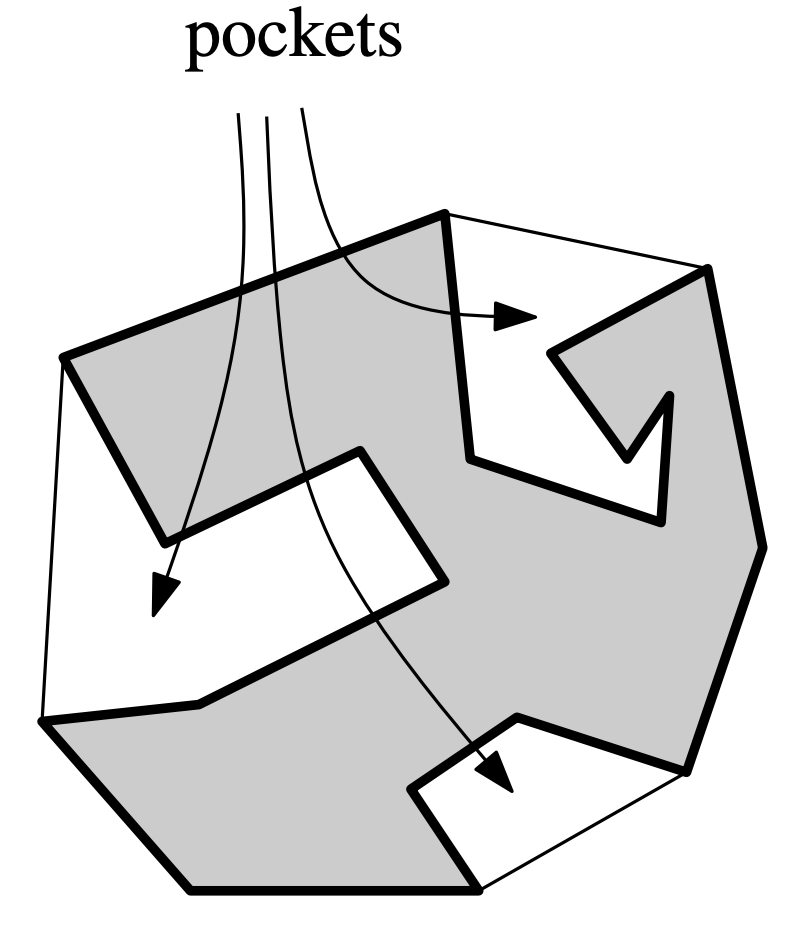Problem 3.12 from the CGAA book describes the pockets of a convex simple polygon as the areas outside the polygon, but inside its convex hull, as shown in the diagram to the right.

Your task is to write a program that loads a file containing the vertices of 2D simple polygon. Remember that a simple polygon may be non-convex, but the edges do not self-intersect, and the shape does not have any interior holes.

Your program should use CGAL 2D Triangulations to create a triangulation of both the input polygon and the pockets. These triangulations will allow you to calculate the area of the input polygon and the sum of the areas of the pockets. It will also allow you to calculate the perimeter of the original polygon, the sum of the lengths of all boundary edges of the input polygon that line or touch the inside of these pockets, and the sum of the lengths of the boundary edges that are added to form the convex hull of the input points.

Your program will output the triangulation to a file named output_pockets.off and write the area and perimeter statistics to output_stats.txt. Here is the sample command line: 

./pocket_triangulation ../src/input_sample_polygon.txt output_sample_stats.txt output_sample_polygon.off output_sample_pockets.off

Here are sample input and output files:

The input file starts with the number of polygons contained in the input (for connected inputs, this will always be '1'). Next, for each input polygon, the number of vertices are listed, followed by the number of interior holes (for simple polygons, the number of holes will always be zero). Then the x and y coordinates for each point are listed. After the coordinates for the outer boundary of the polygon are finished, the geometry for each hole is listed. First, the number of points for that hole, then the x and y coordinates each point.

After you finish writing the output files, your program should use the CGAL::draw function (also used for the previous homework) to visualize the triangulation of the original polygon, and then in second popup window, the triangulation of the pockets. See the draw_surface_mesh example. Note that these functions are blocking, so make sure you have finished writing the output files before launching this viewer.

Note of course that there are multiple ways to validly triangulate most polygonal outlines. Your program may return any valid triangulation.

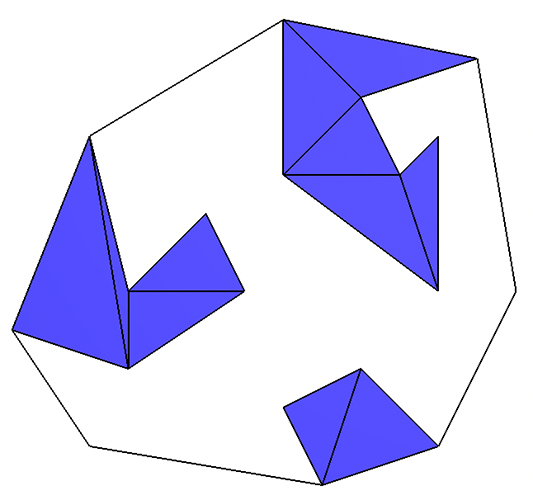
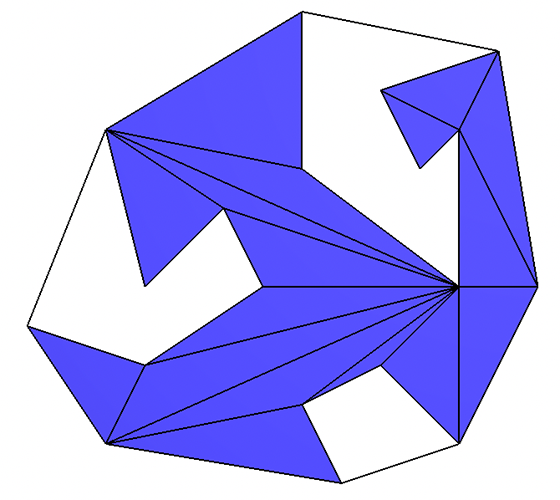
Part 3: Handle Non-Simple Polygons - OPTIONAL Extra Credit

For extra credit, extend your implementation for Part 2 to handle input polygons that are disconnected (two or more separate, non-overlapping polygons) and polygons with interior holes.

Part 4: Analysis of Implementation

In your hw3_polygon_triangulations.pdf file, analyze the running time of your implementation for Part 2 (and optionally Part 3), in terms of n, the number of edges in the input polygon; p, the count of the number of pockets; c, the number of edges on the convex hull; e, the number of edges on the input polygon that line or touch the pockets, i_t the number of triangles on the input triangulation, and p_t the number of triangles that fill the pockets.

In addition to your Big O Notation Analysis of the running time, discuss the relationships (equal/greater than/less than/etc) between these variables.