Homework 5: k-D Trees and Range Trees

Part 1: Book Problems

Prepare a PDF file named hw5_kdtrees_and_range_trees.pdf with your answers to the book problems below. You may use Latex, Google Docs (export/save as PDF), MS Word (export/save as PDF), and/or legibly handwrite on paper and scan to PDF.

From "Computational Geometry: Algorithms and Applications", de Berg, Cheong, van Kreveld, and Overmars.

You may discuss these problems with your classmates, but you must write up your solutions individually. Note the names of anyone you talked to or collaborated with in your hw5_kdtrees_and_range_trees.pdf writeup.

Please do not search for solutions or notes published by the authors or any instructor or notes or solutions shared by other students on the internet. Any use of these types of materials is considered a violation of Academic Integrity for this course.

5.6
Describe algorithms to insert and delete points from a range tree. You don't have to take care of rebalancing the structure.

5.8a,b
Theorem 5.8 showed that a range tree on a set of n points in the plane requires O(n log n) storage. One could bring down the storage requirements by storing associated structures only with a subset of the nodes in the main tree.
a. Suppose that only the nodes with depth 0, 2, 4, 6, ... have an associated structure. Show how the query algorithm can be adapted to answer queries correctly.
b.Analyze the storage requirements and query time of such a data structure.

5.10a,b
In some applications one is interested only in the number of points that lie in a range rather than in reporting all of them. Such queries are often referred to as range counting queries. In this case one would like to avoid having an additive term of O(k) in the query time.
a. Describe how a 1-dimensional range tree can be adapted such that a range counting query can be performed in O(log n) time. Prove the query time bound.
b. Using the solution to the 1-dimensional problem, describe how d-dimensional range counting queries can be answered in O(log^d n) time. Prove the query time.

Part 2: CGAL Programming Task

Lidar or "light detection and ranging" technology is used to collect 3D points, a.k.a., a point cloud, of objects in the world around us. It can be used to scan the exteriors or interiors of buildings, as shown in the examples below. Note that the scan points have some uncertainty or noise in the point position and we have holes or missing data when objects are occluded or shadowed by other parts of the scene.

A common task is to collect all points near a query point x,y,z and estimate the local surface geometry, specifically the surface normal. This is helpful in eventually accomplishing the ultimate goal of converting the point cloud to a polygonal surface mesh.

Your task is to write a program that loads a point cloud, a large set of 3D points, from an input file and stores them in a CGAL kD tree. You will then process a list of queries against the kD tree one at a time. For each of these query points you will collect the c data points closest to that query position and give a rough estimate of the surface geometry at that position. We will assume that the surface is axis-aligned -- that is, it is parallel to the xy, yz, or xz plane.

For each query point you will output the best match plane (xy, yz, or xz), and the minimum radius necessary to capture exactly c points within a circle of that radius in the specified plane, with a tolerance or error in the perpendicular axis of no more than plus or minus t units. The values of c and t will be provided on the command line.

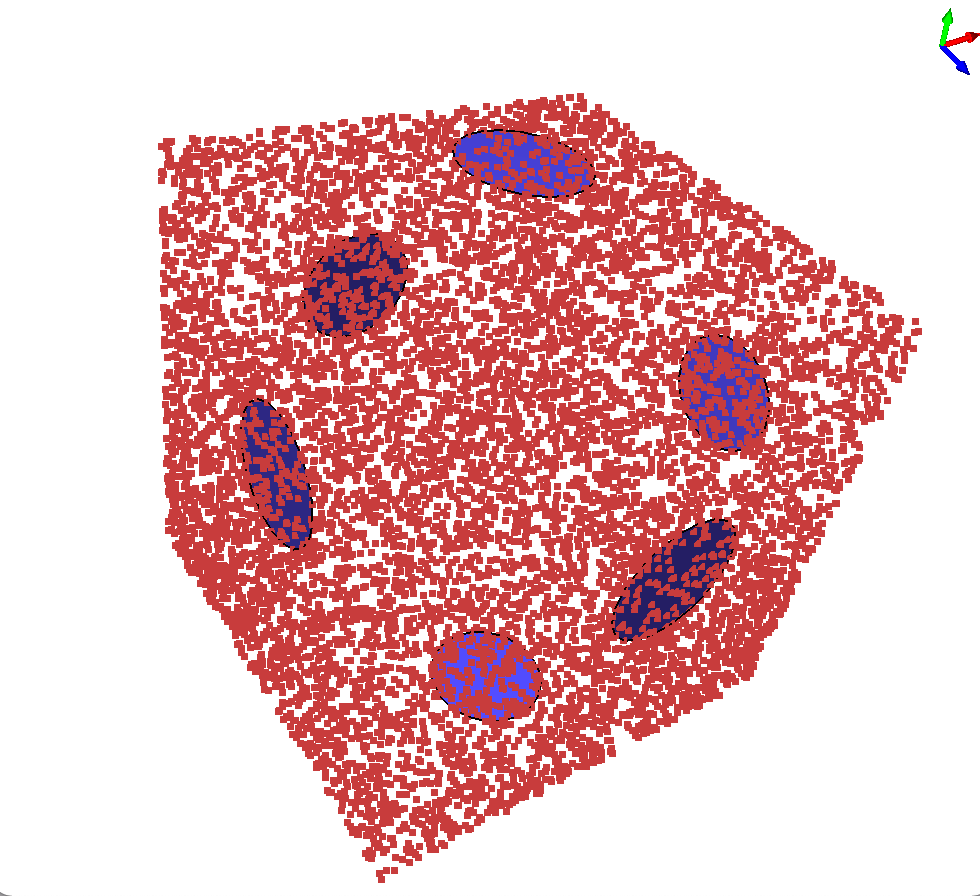
For example, we will start with a point cloud of 10,000 randomly distributed points on the surface of a cube from (-10,-10,-10)->(10,10,10). We are given 6 query points, one near the middle of each of the 6 faces of the cube. Once we determine the best matching axis-aligned plane, we determine the tightest radius around that query point that captures c=100 points with tolerance +/- 0.01 distance from that plane.

  ./detect_point_cloud_surface input_cube_points.txt input_cube_queries.txt 100 0.01 output_cube_stats.txt

After outputting the statistics file above, your program can use the CGAL Surface Mesh visualization to draw both the input point cloud data AND simple polygonal representation of the circles, as shown below. Note that pressing 'v' will draw the vertices.

Additional test data:

Be sure to try different values for c, the target number of points to capture and the tolerance t.

Part 3: Analysis of Implementation

In your hw5_kdtrees_and_range_trees.pdf file, analyze the running time of your implementation for Part 2, in terms of n, the number of points in the point cloud, and c the number of points that must be collected. You may introduce other variables as necessary.