recitation 19: review for quiz 2
========================================================================
Memoization is a clever idea that allows us to save on computation. It
works by keeping track of evaluation of a procedure on a specific
argument, and simply returns the remembered value if the procedure has
already been run on that argument.
(define (memoize proc)
(let ((cache '()))
(lambda (arg)
(if (assq arg cache)
(cadr (assq arg cache))
(let ((answer (proc arg)))
(set! cache (cons (list arg answer) cache))
answer)))))
(define my-sq (memoize (lambda (x) (* x x))))
(my-sq 5)
Finish the environment diagram:
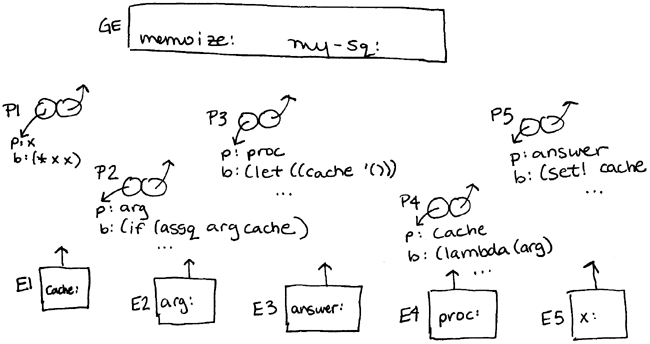
To what does the environment pointer of P1 point?
To what does the environment pointer of P2 point?
To what does the environment pointer of P3 point?
To what does the environment pointer of P4 point?
To what does the environment pointer of P5 point?
What is the enclosing environment for E1?
What is the enclosing environment for E2?
What is the enclosing environment for E3?
What is the enclosing environment for E4?
What is the enclosing environment for E5?
To what is the variable memoize in the global environment bound?
To what is the variable my-sq in the global environment bound?
To what is the variable cache in E1 bound?
To what is the variable arg in E2 bound?
What variable is bound to the procedure object P1?
Give both the name and the environment.
What variable is bound to the procedure object P5?
Give both the name and the environment.
ANSWERS:
GE, E1, GE, E4, E2,
E4, E1, E2, GE, GE,
P3, P2, ((5 25)), 5,
proc in E4, nothing
========================================================================
what code made this environment diagram? (some parts may not be drawn)
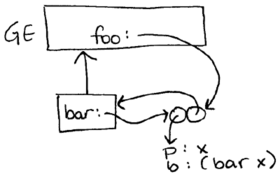
(define foo
(let ((bar nil))
(set! bar (lambda (x) (bar x)))
bar))
OR
(define foo
(let ()
(define bar (lambda (x) (bar x)))
bar))
what code made this cons cell structure?
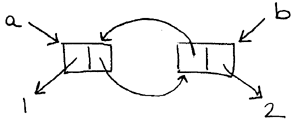
(define a (cons 1 (cons nil 2))
(define b (cdr a))
(set-car! b a)
========================================================================
* let's write insertion sort:
(define lst (make-sorted-list))
(get-data lst) -> ()
(insert lst 4)
(insert lst 1)
(get-data lst) -> (1 4)
(insert lst 5)
(insert lst 6)
(insert lst 7)
(insert lst 3)
(get-data lst) -> (1 3 4 5 6 7)
(define (make-sorted-list)
(cons 'sorted '()))
(define (get-data sorted-list)
(if (eq? (car sorted-list) 'sorted)
(cdr sorted-list)
(error "not a sorted-list")))
(define (insert sorted-list element)
(cond ((null? (cdr sorted-list))
(set-cdr! sorted-list (cons element nil)))
((< element (cadr sorted-list))
(set-cdr! sorted-list (cons element (cdr sorted-list))))
(else (insert (cdr sorted-list) element))))
* whats the order of growth?
Order of growth: O(n^2)
* say we know that often the elements are often inserted in clumps
that are already sorted (either increasing or decreasing). let's
change the implementation to instead use a "doubly-linked list".
(what's a doubly-linked-list???)
Instead of just a regular list with a pointer to the next element,
there are also pointers to the previous element. This requires alot
more work to maintain a consistent data structure. Here are some
helper functions for one possible implementation:
(define (make-link element)
(cons element (cons nil nil)))
(define (get-element link)
(car link))
(define (get-prev link)
(car (cdr link)))
(define (get-next link)
(cdr (cdr link)))
(define (set-prev! link prev)
(set-car! (cdr link) prev))
(define (set-next! link next)
(set-cdr! (cdr link) next))
and a sorting routine based on this could look like:
(define (make-sorted-list)
(cons 'sorted nil))
(define (get-data sorted-list)
(define (find-front link)
(if (null? (get-prev link))
link
(find-front (get-prev link))))
(define (extract link)
(if (null? link)
nil
(cons (get-element link)
(extract (get-next link)))))
(if (null? (cdr sorted-list))
nil
(extract (find-front (cdr sorted-list))))))
(define (insert sorted-list element)
(let ((current (cdr sorted-list))
(new-unit (make-link element)))
(cond ((null? current)
;; this is the first element
(set-cdr! sorted-list new-unit))
((and (< element (get-element current))
(null? (get-prev current)))
;; add it to the front
(set-next! new-unit current)
(set-prev! current new-unit)
(set-cdr! sorted-list new-unit))
((and (>= element (get-element current))
(null? (get-next current)))
;; add it to the end
(set-prev! new-unit current)
(set-next! current new-unit)
(set-cdr! sorted-list new-unit))
((and (< element (get-element current))
(>= element (get-element (get-prev current))))
;; add the element just in front of the current element
(set-prev! new-unit (get-prev current))
(set-next! new-unit current)
(set-next! (get-prev current) new-unit)
(set-prev! current new-unit)
(set-cdr! sorted-list new-unit))
((< element (get-element current))
;; shift the current pointer to the prev element
(set-cdr! sorted-list (get-prev current))
(insert sorted-list element))
(else
;; shift the current pointer to the next element
(set-cdr! sorted-list (get-next current))
(insert sorted-list element)))))
========================================================================
from Spring 2002, quiz 2
(define x (list a b))
(define y (cons c (cdr x)))
(set-cdr! (cdr x) (list d))
(list x y) ==>
(define x (list a b))
(define y (list c d))
(set-car! y a)
(set-cdr! y (cdr x))
(eq? x y) ==>
========================================================================
from Fall 1999, quiz 2
Suppose we want a procedure prev with the property that it returns the
previous value it was applied to. For example:
(prev 1) ==> undef
(prev 2) ==> 1
(prev 3) ==> 2
Which of the following attempts to implement prev works correctly?
(you probably want to draw an environment diagram for each)
(define prev1
(let ((x 'undef))
(lambda (y)
(let ((z x))
(set! x y)
z))))
(define prev2
(let ((x (list 'undef)))
(lambda (y)
(let ((z x))
(set-car! x y)
(car z)))))
(define prev3
(let ((x (cons 'undef 'undef)))
(lambda (y)
(set-car! x (cdr x))
(set-cdr! x y)
(car x))))
Suppose we have a correctly implemented version of prev. What is the
result of evaluating the expressions below? Assume a fresh evaluation
of our prev definition for each.
(let ((x (prev prev)))
(((prev +) prev) 1 2))
(let ((foo (prev prev)))
(((foo +) foo) 1 2))
(let ((g (prev prev))
(f (prev prev)))
(((f +) f) 1 2))
========================================================================
from Fall 2002, quiz 2
(define (make-queue elt)
(let ((temp (list elt)))
(cons temp temp)))
(define (head q) (car q))
(define change-head! set-car!)
(define (tail q) (cdr q))
(define change-tail! set-cdr!)
(define (read q) (car (head q)))
(define my-queue (make-queue 1))
my-queue ==> ((1) 1)
(read my-queue) ==> 1
(add-queue 2 my-queue)
my-queue ==> ((1 2) 2)
(read my-q) ==> 1
(add-queue 3 my-queue)
my-queue ==> (1 2 3) 3)
(delete-queue my-queue)
my-queue ==> ((2 3) 3)
(read my-q) ==> 2
(delete-queue my-queue)
my-queue ==> ((3) 3)
(delete-queue my-queue)
my-queue ==> (#f)
* finish the definition of add-queue:
(define (add-queue elt q)
(let ((new-part (list elt)))
(cond ((null? (tail q))
INSERT-1)
(else
INSERT-2
INSERT-3)))
q)
* finish the definition of delete-queue:
(define (delete-queue q)
(cond ((eq? (head q) (tail q))
(change-head! q #f)
(change-tail! q #f))
(else INSERT-4))
q)
* Draw a box and pointer diagram for the value of my-queue for the
above sequence of actions.
* Suppose we decide to change the underlying representation of a
queue, to use a list rather than a pair to represent the head and
tail of the queue (as below). What else must change?
(define (make-queue elt)
(let ((temp (list elt)))
(list temp temp)))


