Scheme examples & Exercise 0

Scheme examples

Here's the factorial example I wrote in class today:

(define (factorial N)
  (if (zero? N)
      1
      (* N (factorial (- N 1)))))

Recall that the recursive formulation is:

N! = N * (N-1)!   if N>0
   = 1            otherwise

Note that the Scheme procedure directly follows the (recursive) mathematical definition.

I also wrote the factorial procedure a different way in class. As I was writing this web page, I came up with a (mostly) better way. Here it is instead of what I wrote in class:

(define (factorial N)
  (if (= N 0)
      1
      (fac 1 N)))

(define (int-products x y)
  (if (= x y)
      x
      (* x (int-products (+ x 1) y))))

This example is not as elegant as the first implementation because the factorial function has to check for a special case. The int-products procedure implements a function, let's call it f(x,y) that computes the product of the integers from x to y (inclusive). Therefore its recursive formulation is:

f(x,y) = x * f(x+1, y)    if x<=y
       = x                if x=y

Again, the scheme implementation follows this recursive definition directly. Note that it is not defined for x>y. Its Scheme implementation would enter an infinite loop. One of the points of this example is that you can (and sometimes need to) use a helper procedure — your main procedure does something very simple (often just calling the helper procedure with the proper arguments) and then the helper procedure does all the work.

Exercise 0

This is the exercise that I didn't get to in class today:

Write a recursive Scheme procedure (approx-pi N)which calculates an approximation to pi using the first (N+1) terms, i.e., i=0 through i=N, of the following series:

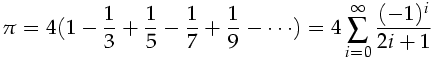
for example:

> (approx-pi 0)
;Value: 4
> (approx-pi 1)
;Value: 8/3

Try it yourself first; you can see my solution if you're stuck.

Note that this is very similar to problem 10 on assignment 1.